Trần Thị Minh Hải
Trường Đại học Kinh tế Kỹ thuật Công nghiệp
Cao Lan Phương, Mai Anh Vũ
Trường Đại học Văn hóa Thể thao Du lịch Thanh Hóa
(Quanlynhanuoc.vn) – Trong bối cảnh ngành du lịch Việt Nam đang trên đà phục hồi và tăng trưởng mạnh mẽ sau đại dịch, việc dự báo chính xác lượng khách quốc tế đã trở thành một yêu cầu cấp thiết cho công tác hoạch định chính sách và chiến lược phát triển. Nghiên cứu này ứng dụng mô hình tự hồi quy tích hợp trung bình trượt (ARIMA) để xây dựng một công cụ dự báo định lượng khoa học, nhằm ngoại suy xu hướng lượt khách quốc tế đến Việt Nam trong tương lai gần. Kết quả nghiên cứu cho thấy, mô hình ARIMA (6,1,2) đã được xác định là mô hình tối ưu nhất để dự báo lượt khách quốc tế đến Việt Nam. Kết quả này là cơ sở khoa học cho các nhà hoạch định, nhà quản lý tham khảo cho việc thực hiện triển khai các kế hoạch đầu tư về cơ sở vật chất, nguồn lực,… phục vụ cho ngành du lịch nhằm đáp ứng được tốt nhất nhu cầu của du khách.
Từ khóa: ARIMA, khách Du lịch quốc tế, Việt Nam, Quý IV/2025, Quý I/2026.
1. Đặt vấn đề
Trong bối cảnh toàn cầu hóa, ngành du lịch đã và đang khẳng định vai trò là một trong những động lực tăng trưởng kinh tế – xã hội then chốt trên toàn thế giới. Tổ chức Du lịch Thế giới (UNWTO) nhấn mạnh vai trò quan trọng của du lịch trong việc tạo ra việc làm, thúc đẩy phát triển cơ sở hạ tầng và tăng cường giao lưu văn hóa giữa các quốc gia. Trong những năm gần đây, Việt Nam đã nổi lên như một điểm đến hấp dẫn và an toàn trên bản đồ du lịch quốc tế, ghi nhận sự phục hồi và tăng trưởng ngoạn mục sau đại dịch Covid-19. Theo thống kê của Cục Du lịch Quốc gia Việt Nam, chỉ riêng năm 2023, Việt Nam đã đón 12,6 triệu lượt khách quốc tế, tổng thu từ du lịch ước đạt 678 nghìn tỷ đồng. Điểm nổi bật là, trong giai đoạn phát triển ổn định trước dịch bệnh Covid-19 (năm 2019), lượt khách quốc tế đến Việt Nam chỉ chiếm 17% tổng lượt khách nhưng lại đóng góp chính trong danh mục danh thu toàn ngành, điều này khẳng định vị thế là “huyết mạch” kinh tế của du lịch Việt Nam. Chính vì vậy, việc đạt và vượt các mục tiêu về thu hút khách quốc tế không chỉ góp phần trực tiếp vào tổng sản phẩm quốc nội (GDP) và cân bằng cán cân ngoại tệ, mà còn tạo hiệu ứng lan tỏa, thúc đẩy sự phát triển bền vững của các ngành dịch vụ liên quan như hàng không, lưu trú cao cấp và bán lẻ.
Tuy nhiên, sự thành công của ngành du lịch, đặc biệt là ở mảng khách quốc tế, luôn song hành với những thách thức không nhỏ. Nhu cầu du lịch quốc tế vốn có đặc tính cố hữu là sự nhạy cảm cao và dễ bị tác động bởi các yếu tố ngoại sinh khó lường (Song và cộng sự, 2019). Các cuộc khủng hoảng kinh tế toàn cầu, bất ổn địa chính trị, các vấn đề về y tế công cộng như đại dịch, hay thậm chí là các biến động về tỷ giá hối đoái đều có khả năng gây ra những thay đổi đột ngột và có nhiều khó khăn trong việc dự báo lượt khách quốc tế. Giai đoạn 2020- 2022 là minh chứng rõ nét nhất khi các biện pháp hạn chế đi lại toàn cầu đã khiến ngành du lịch gần như “tê liệt”, gây ra thiệt hại nặng nề cho các doanh nghiệp và nền kinh tế. Thực tế này cho thấy, công tác dự báo lượng khách du lịch quốc tế là một bài toán phức tạp và mang tính thách thức cao đối với các nhà hoạch định chính sách và quản lý ngành.
Trong bối cảnh đầy biến động đó, việc ra quyết định chiến lược dựa trên kinh nghiệm chủ quan hay các phương pháp thống kê mô tả đơn thuần không còn đủ độ tin cậy. Để có thể chủ động trong việc lập kế hoạch phát triển, từ việc phân bổ nguồn lực cho các chiến dịch quảng bá, xúc tiến du lịch tầm quốc gia, đến việc định hướng đầu tư vào cơ sở hạ tầng lưu trú và dịch vụ, đòi hỏi phải có một công cụ dự báo định lượng khoa học. Một công cụ hiệu quả cần có khả năng “học” từ các quy luật và mẫu hình ẩn chứa trong dữ liệu quá khứ để ngoại suy ra các xu hướng trong tương lai gần.
Đáp ứng yêu cầu này, mô hình tự hồi quy tích hợp trung bình trượt- ARIMA (Autoregressive Integrated Moving Average), do (Box & Jenkins, 1976) phát triển, được công nhận rộng rãi là một phương pháp luận mạnh mẽ và hiệu quả trong phân tích chuỗi thời gian. Về bản chất, ARIMA phân tích cấu trúc phụ thuộc nội tại của một chuỗi dữ liệu, cho phép mô hình hóa và dự báo giá trị tương lai dựa trên chính các giá trị trong quá khứ và các sai số ngẫu nhiên. Tính ưu việt và vai trò là một “mô hình nền tảng” trong lĩnh vực dự báo du lịch đã được kiểm chứng và tổng kết qua rất nhiều công trình nghiên cứu trên thế giới (Song & Li, 2008).
Xuất phát từ những luận điểm trên, việc ứng dụng một mô hình đã được kiểm chứng về độ tin cậy và tính hiệu quả như ARIMA để phân tích và dự báo là hoàn toàn cần thiết và có cơ sở khoa học. Vì vậy, nghiên cứu này được thực hiện nhằm mục tiêu sử dụng mô hình ARIMA để xây dựng và kiểm định mô hình dự báo lượt khách quốc tế đến Việt Nam trong quý IV năm 2025 và quý I năm 2026, qua đó cung cấp một nguồn tham khảo định lượng hữu ích cho các cơ quan quản lý nhà nước và các bên liên quan trong ngành Du lịch.
2. Tổng quan nghiên cứu
Mô hình tự hồi quy tích hợp trung bình trượt ARIMA (Autoregressive Intergrated Moving Average) của Box và Jenkins (1976) được xem là một trong những mô hình điển hình và nền tảng trong việc dự báo chuỗi thời gian trong du lịch, được kiểm chứng độ tin cậy qua nhiều nghiên cứu (Lim & McAleer, 2002). Trong các nghiên cứu sử dụng mô hình ARIMA, có thể khái quát lại thành các nhóm tiếp cận sau:
Nhóm các nghiên cứu thực hiện sử dụng nhiều mô hình dự báo chuỗi thời gian khác nhau để cùng kiểm định cho một dữ liệu nghiên cứu, nhằm tìm ra mô hình tối ưu nhất cho một chuỗi dữ liệu cụ thể, hoặc sử dụng kết quả của các mô hình để bổ trợ trong việc đưa ra các chiến lược. Theo (Goh & Law, 2002) nhóm tác giả sử dụng đồng thời mô hình ARIMA theo mùa với các mô hình san bằng mũ để thực hiện dự báo lượng khách du lịch đến Hồng Kông. Kết quả cho thấy, mô hình ARIMA theo mùa vụ cho dự báo với khả năng chính xác cao hơn trong việc nắm bắt được các yếu tố mùa vụ phức tạp. Dẫn theo (Chu, 2009) sử dụng chính các biến thể khác nhau của mô hình ARIMA trong việc xác định các tham số (p,d,q) để đưa ra được mô hình dự báo tốt nhất trong việc dự báo lượng khách du lịch đến một số địa điểm ở khu vực châu Á- Thái Bình Dương. Trong nghiên cứu của (Bình và cộng sự, 2023) sử dụng đồng thời mô hình ARIMA và mô hình “Growth” trong việc dự báo lượng khách du lịch quốc tế đến Bình Định để làm cơ sở căn cứ đưa ra các quyết địn chiến lược trong việc đầu tư cở sở hạ tầng, chuẩn bị nguồn nhân lực. Mô hình ARIMA là một trong những mô hình cho kết quả dự báo chính xác lượng khách du lịch tham quan ba công viên Quốc gia lớn của Hoa Kỳ, (Chen và cộng sự, 2008).
Một số nghiên cứu khác sử dụng mô hình ARIMA để dự báo lượng khách du lịch với không gian địa điểm khác nhau lại cho ra những kết luận khác nhau. Theo (Karadzic & Pejovic, 2020), mô hình ARIMA(8,1,5) là mô hình dự báo tốt nhất để dự báo lượng khách du lịch đến Montenegro. Tác giả (Petrevska, 2017), cho rằng mô hình ARIMA(1, 1, 1) là mô hình phù hợp nhất để dự báo lượng khách du lịch quốc tế đến Cộng hòa Macedonia. Bên cạnh đó, (Giám và cộng sự, 2012) lại chỉ ra rằng, mô hình ARIMA(12,1,12) là mô hình tốt nhất để dự báo lượng khách du lịch quốc tế đến Việt Nam. Trong nghiên cứu của (Nghiêm, 2017) sử dụng một biến thể của ARIMA là SARIMA để dự báo khách quốc tế đến Việt Nam thu được kết quả khả thi. (Cho, 2001) sử dụng ba kỹ thuật biến thể khác nhau của mô hình ARIMA để dự báo lượng khách du lịch đến Hồng Kông từ các quốc gia khác nhau. Kết quả cho thấy phương pháp dự báo ARIMA điều chỉnh là phương pháp dự báo tối ưu nhất cho Nhật Bản, còn ARIMA đơn biến là phương pháp dự báo phù hợp với thị trường Hoa Kỳ và Vương quốc Anh. Đối với thị trường Đài Loan, Singapore và Hàn Quốc, mô hình ARIMA đơn biến và điều chỉnh cho kết quả dự báo tương đồng. Vì vậy, nghiên cứu này kết luận mô hình ARIMA đơn biến và điều chỉnh là phù hợp để dự báo chuỗi biến động của lượng du khách.
Trên cơ sở các công trình nghiên cứu đã công bố, nhận thấy mô hình ARIMA có độ tin cậy tốt trong việc sử dụng để dự báo lượng khách du lịch đến một điểm đến nhất định. Tuy nhiên, với mỗi nghiên cứu khác nhau, trong các thị trường Du lịch khác nhau lại cho ra những kết luận khác nhau. Vì vậy, kết quả dự báo cho điểm đến này không thể “tái sử dụng” cho điểm đến khác. Đặc biệt, cho đến nay nhóm tác giả chưa thấy có công trình nghiên cứu chuyên sâu nào sử dụng mô hình ARIMA để dự báo lượt khách quốc tế đến Việt Nam vào quý IV năm 2025 và quý I năm 2026. Vì thế, thực hiện triển khai công trình này là hoàn toàn cần thiết và khả thi. Nghiên cứu sẽ cung cấp các luận cứ khoa học đầu tiên về sự biến động của chuỗi thời gian của lượt khách quốc tế đến Việt Nam. Kết quả nghiên cứu là nguồn tham khảo tin cậy cho các nhà hoạch định chính sách, các nhà quản lý doanh nghiệp Du lịch.
3. Phương pháp nghiên cứu
Phương pháp Box- Jenkins do hai nhà nghiên cứu George và Gwilym Jenkins phát triển vào năm 1976. Phương pháp này cung cấp một quy trình có hệ thống để nhận diện, ước lượng và kiểm định các biến thể của mô hình ARIMA trong việc phân tích và dự báo chuỗi thời gian. Nền tảng của mô hình này dựa trên giả định rằng các giá trị tương lai của chuỗi thời gian có thể được dự báo một cách hiệu quả thông qua việc phân tích tương quan tuyến tính của nó với các giá trị trong quá khứ và các sai số ngẫu nhiên. Nhờ vào khả năng phân tích này, mô hình ARIMA trở thành công cụ dự báo ngắn hạn trong nhiều lĩnh vực như kinh tế, kỹ thuật…
Mô hình ARIMA tổng quát được biểu diễn bởi ba thành phần: tự hồi quy (AR) được ước lượng qua tham số (p), bậc sai phân (I) ước lượng qua tham số (d), trung bình trượt (MA) ước lượng qua tham số (q). Theo các nhà nghiên cứu (Gujarati & Porter, 2004), (Adkins & Hill, 2011), Tran & Mai (2025) mô hình này được tiến hành xây dựng thông qua 04 bước cơ bản sau:
Bước 1: Xác định mô hình
Giai đoạn này tập trung vào việc xác định các tham số (p, d, q) của mô hình.
Bậc sai phân I(d) được xác định qua việc kiểm tra tính dừng của chuỗi dữ liệu bằng cách thực hiện kiểm định Dickey- Fuller (ADF). Nếu chuỗi dừng tại bậc (0) thì giá trị của (d=0), tương tự với sai phân bậc 1 thì I(d=1), sai phân bậc 2 thì I (d=2),… quá trình này được thực hiện cho tới khi chuỗi dừng.
Bậc (p) và (q) của mô hình được xác định khi chuỗi đã dừng. Thực hiện phân tích biểu đồ tự tương quan (ACF) và tự tương quan riêng phần (PACF).
Quá trình tự hồi quy AR(p) thể hiện sự phụ thuộc tuyến tính của giá trị hiện tại Xt vào giá trị quá khứ của nó.
Xt = β0 + β1xt-1 + β2xt-2 + … + βpxt-p (1)
Trong đó: Xt chuỗi cần dự báo, xt là sai số của mô hình.
Dựa vào biểu đồ ACF, PACF cho biết giá (p), nếu chuỗi có dạng AR(p) thì hệ số tương quan riêng phần của biểu đồ PACF có ý nghĩa thống kê với giá trị từ 1 đến (p) và các giá trị sau giảm nhanh về 0, lúc này biểu đồ ACF biểu diễn các hệ số tương quan giảm dần về giá trị 0.
Quá trình MA(q), của chuỗi Xt được biểu biễn như sau:
Xt = € + α0xt + α 1xt-1 + α 2xt-2 + … + α qxt-q (2)
Biểu đồ ACF có hệ số tương quan có ý nghĩa thống kê với độ trễ từ 1 đến (q) nếu chuỗi có dạng MA(q), các giá trị sau tiến về 0 và biểu đồ PACF sẽ biểu diễn các hệ số tương quan riêng phần tiến về 0.
Kết hợp (1) và (2) ta có mô hình ARMA (p, q) như sau:
Xt = € + α0xt + α 1xt-1 + α 2xt-2 + … + α qxt-q + β0xt + β1xt-1 + β 2xt-2 + … + βqxt-q (3)
Bước 2: Ước lượng mô hình
Phân tích dữ liệu trên phần mềm EViews 12 để xác định các đại lượng (p,q) của mô hình ARIMA. Dựa trên việc so sánh các giá trị R2 hiệu chỉnh, AIC- Akaike info criterion, Log likelihood, Schwarz của các biến thể của mô hình ARIMA cho đến khi xác định được mô hình tối ưu nhất.
Bước 3: Kiểm định mô hình
Mô hình được xem là phù hợp và đáng tin cậy nếu sai số là nhiễu trắng. Điều này có nghĩa là phần dư không được chứa bất kỳ thông tin hay quy luật nào có thể giải thích thêm. Để kiểm tra giả định này, bằng phương pháp trực quan được xác định qua biểu đồ tự tương quan (ACF) của chuỗi phần dư, nếu mô hình là tối ưu thì tất cả các cột tương quan (ngoại trừ độ trễ 0) phải nằm trong khoảng tin cậy. Ngoài ra, bằng phương pháp thống kê có thể sử dụng kiểm định Breusch- Godfrey để phát hiện tự tương quan bậc cao hơn. Trong trường hợp có phương sai của sai số thay đổi thì thực hiện kiểm định White hoặc kiểm định ARCH.
Bước 4: Giai đoạn dự báo
Sau khi mô hình đã được xác định và kiểm định, bước cuối cùng là thực hiện dự báo. Năng lực dự báo của mô hình được đánh giá qua hai loại dự báo: dự báo trong mẫu nhằm kiểm tra độ khớp với dữ liệu quá khứ và dự báo ngoài mẫu để ước tính các giá trị trong tương lai. Sự thỏa đáng của mô hình được tái khẳng định qua các biểu đồ ACF và PACF của phần dư không cho thấy bất kỳ hệ số tương quan nào có ý nghĩa thống kê với tất cả các giá trị nằm trong khoảng tin cậy.
4. Kết quả nghiên cứu
Để thực hiện nghiên cứu, nhóm tác giả tiến hành thu thập, xây dựng bộ dữ liệu về chuỗi thời gian của lượng khách quốc tế đến Việt Nam. Dữ liệu được tổng hợp từ Tổng Cục Thống kê Việt Nam, thời gian lấy mẫu từ tháng 01/2020 – 8/2025. Toàn bộ dữ liệu được nhập liệu và xử lý trên phần mềm EViews 12. Quá trình kiểm định mô hình ARIMA dự báo lượt khách quốc tế đến Việt Nam vào quý IV năm 2025 và quý I năm 2026 được mô tả như tiến trình sau:
4.1. Xác định mô hình
Mô hình ARIMA được áp dụng nếu chuỗi thời gian có tính dừng. Thực hiện kiểm định ADF của chuỗi lượt khách du lịch quốc tế đến Việt Nam với sai phân bậc 0, kết quả thu được giá trị t-Statistic lớn hơn các giá trị tới hạn với mức ý nghĩa 1%, 5% và giá trị Prob*. = 0.0709 > 0.05 nên kết luận được chuỗi lượt khách quốc tế đến Việt Nam là không dừng. Kết quả được thể hiện như bảng 1:
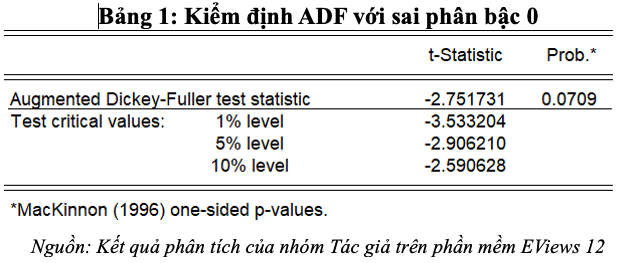
Tại sai phân bậc 0, chuỗi thời gian của lượt khách quốc tế đến Việt Nam là không dừng. Vì vậy, tiếp tục thực hiện kiểm định ADF với sai phân bậc 1. Kết quả như bảng 2 dưới đây:
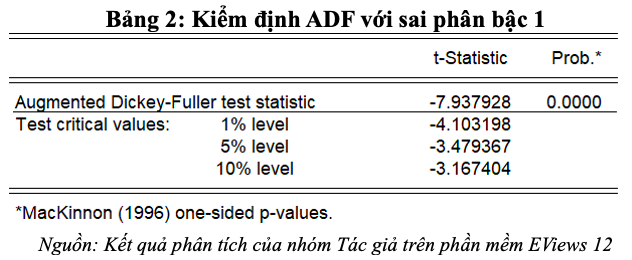
Kết quả tại bảng 2 cho thấy các giá trị t-Statistic đều lớn hơn các giá trị tới hạn, giá trị Prob*. = 0.0000 < 0.05 nên kết luận chuỗi thời gian của lượt khách quốc tế đã dừng.
Vì chuỗi thời gian của lượt khách đã có điểm dừng nên mô hình ARIMA được áp dụng. Để xây dựng mô hình này, nhóm tác giả tiến hành xác định giá trị (p); (q), hai giá trị này được xác định dựa trên biểu đồ tự tương quan ACF và tự tương quan riêng phần PACF. Phân tích mô hình chuỗi dừng với sai phân bậc 1 thu được kết quả được thể hiện trong bảng 3.

4.2. Ước lượng tham số
Các tham số (p, d, q) được xác định như trên bảng 3, mô hình ARIMA được xây dựng với các biến thể sau: ARIMA (2,1,2); ARIMA (4,1,2); ARIMA (6,1,2); ARIMA (8,1,2). Để xác định được mô hình tối ưu trong các biến thể của mô hình ARIMA này, nhóm tác giả thực hiện kiểm định và so sánh các giá trị R2 hiệu chỉnh, AIC, Log likelihood, Schwarz của các mô hình với nhau. Kết quả thu được bảng tổng hợp sau:
Bảng 4: So sánh các chỉ số R2 hiệu chỉnh, AIC, Log likelihood, Schwarz
| Mô hình | ARIMA (2,1,2) | ARIMA (4,1,2) | ARIMA (6,1,2)* | ARIMA (8,1,2) | Lựa chọn tốt nhất |
| R2 hiệu chỉnh | 0.486892 | 0.486859 | 0.491949 | 0.491018 | Cao nhất |
| Log likelihood | – 467.2579 | – 467.2447 | – 467.0930 | – 467.2049 | Thấp nhất |
| AIC | 14.06740 | 14.06701 | 14.06248 | 14.06582 | Cao nhất |
| Schwarz | 14.19902 | – 467.2049 | 14.19410 | 14.19744 | Thấp nhất |
Trong 04 mô hình là các biến thể của mô hình ARIMA được đưa ra theo như bảng 4. Sau khi so sánh các giá trị R2 hiệu chỉnh, AIC, Log likelihood, Schwarz của các mô hình với nhau, nhận thấy mô hình ARIMA (6,1,2)* được lựa chọn là mô hình tối ưu nhất, vì nó vượt trội hơn các mô hình còn lại dựa trên việc so sánh các tiêu chí R2 hiệu chỉnh, AIC, Log likelihood, Schwarz cụ thể: giá trị R2 hiệu chỉnh cho biết mức độ biến thiên của biến phụ thuộc được giải thích bởi mô hình, giá trị ngày càng cao thì càng tốt.
Mô hình ARIMA (6,1,2) có giá trị R2 =0.491949 là cao nhất so với các mô hình còn lại. Giá trị AIC và Schwarz cho biết sự phức tạp của mô hình và mức độ phù hợp của nó với dữ liệu, giá trị này càng nhỏ thì mô hình này càng tốt. Trong 04 mô hình trên thì mô hình ARIMA (6,1,2) có chỉ số AIC và Schwarz là thấp nhất, điều này cho thấy mô hình có sự cân bằng tốt nhất giữa việc giải thích dữ liệu tránh sự phức tạp không cần thiết.
Chỉ số Log likelihood đo lường mức độ phù hợp của mô hình với dữ liệu quan sát được giá trị này càng cao thì mô hình càng phù hợp. Mô hình ARIMA (6,1,2) có giá trị Log likelihood bằng -0467.0930 là cao nhất so với các mô hình còn lại. Trên cơ sở phân tích này kết luận được rằng mô hình ARIMA (6,1,2) là mô hình tối ưu nhất được sử dụng để dự báo số lượt khách quốc tế đến Việt Nam vào quý IV năm 2025 đến quý I năm 2026.
Tuy nhiên, để khẳng định sự phù hợp của mô hình này trong dự báo lượt khách quốc tế đến Việt Nam thì nhóm tác giả tiếp tục thực hiện phân tích các biểu đồ ACF, PACF của mô hình này. Kết quả được thể hiện như bảng dưới đây:
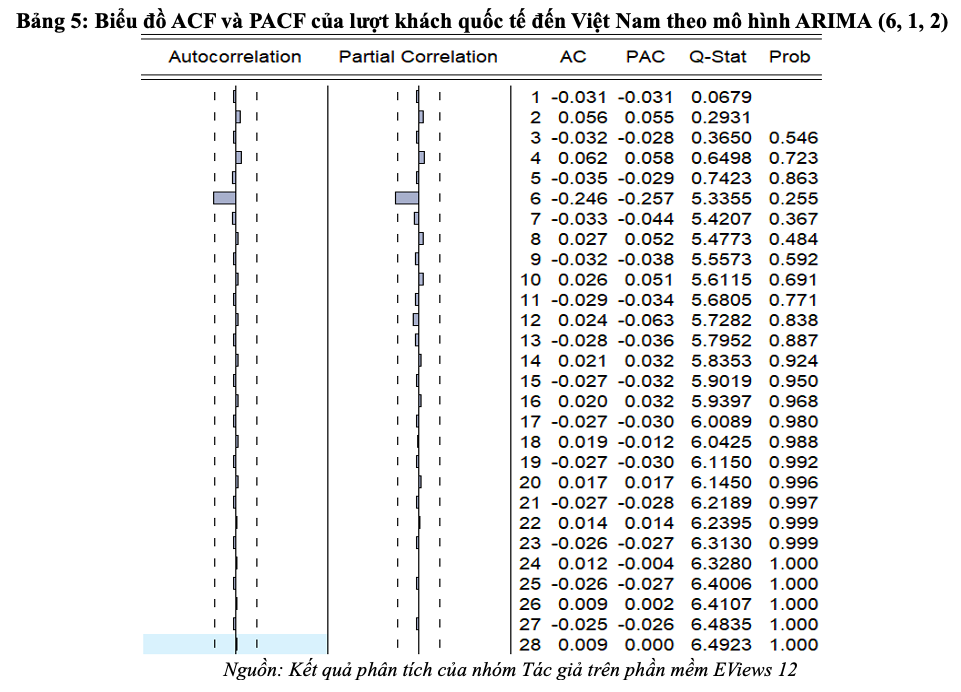
Biểu đồ trong bảng 5 cho thấy, không có giá trị tại độ trễ nào vượt ra khỏi khoảng tin cậy. Vì thế, đây là mô hình tối ưu để dự báo lượt khách quốc tế đến Việt Nam được nghiên cứu này lựa chọn.
4.3. Dự báo
Lượt khách quốc tế đến Việt Nam vào quý IV năm 2025 và quý I năm 2026 được thực hiện dự báo với mô hình ARIMA (6, 1, 2), kết quả dự báo được thể hiện như sau:
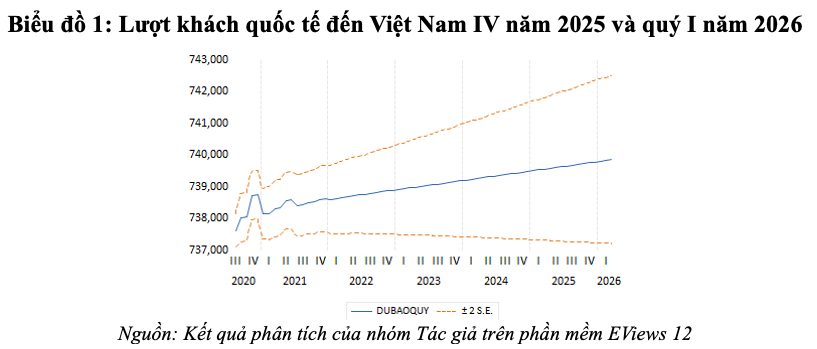
Dựa vào biểu đồ 1, nhận thấy kết quả dự báo lượt khách quốc tế đến Việt Nam, số liệu dự báo cho quý IV năm 2025 và quý I năm 2026 tiếp tục tăng. Trong đó lượng khách quốc tế đến Việt Nam quý IV năm 2025 và lượng khách quốc tế đến Việt Nam quý I năm 2026 trung bình đạt 2,22 triệu lượt.
5. Kết luận
Nghiên cứu đã vận dụng thành công mô hình ARIMA để thực hiện dự báo lượt khách quốc tế đến Việt Nam. Kết quả phân tích chỉ ra mô hình ARIMA (6,1,2) là công cụ hiệu quả và đáng tin cậy nhất để mô hình hóa và dự báo chuỗi dữ liệu này trong số các mô hình được xem xét. Dựa trên mô hình tối ưu đã được lựa chọn, kết quả dự báo cho thấy xu hướng tăng trưởng tích cực và liên tục của lượt khách quốc tế đến Việt Nam trong quý IV năm 2025 và quý I năm 2026. Cụ thể, số lượt khách trung bình trong giai đoạn này được dự báo đạt 2,22 triệu lượt mỗi quý, phản ánh sự phục hồi bền vững và tiềm năng phát triển của du lịch Việt Nam.
Kết quả này không chỉ khẳng định độ tin cậy của phương pháp luận Box-Jenkins trong phân tích chuỗi thời gian của ngành Du lịch mà còn cung cấp một nguồn tham khảo định lượng có giá trị giúp các nhà hoạch định chính sách có thể sử dụng kết quả dự báo này, để chủ động hơn trong việc phân bổ nguồn lực, đầu tư hệ thống cơ sở hạ tầng và triển khai các chiến dịch xúc tiến du lịch hiệu quả, góp phần hiện thực hóa các mục tiêu phát triển kinh tế – xã hội của đất nước.
Tài liệu tham khảo:
1. Bình, C. T., Nguyên, Đ. N. M., Anh, P. L., & Linh, V. T. (n.d.). Phân tích và dự báo sổ khách du lịch quốc tế đến tỉnh Bình Định bằng các mô hình chuỗi thời gian.
2. Giám, Đ. Q., Hân, V. T., Phương, L. T. L., & Thủy, N. T. (2012). Xây dựng mô hình Arima cho dự báo khách du lịch quốc tế đến Việt Nam. Tạp chí Khoa học Nông nghiệp Việt Nam, 10 (2).
3. Nghiêm, P. H. (2017). Ứng dụng mô hình SARIMA dự báo lượng khách quốc tế đến Việt Nam đến năm 2020.
4. Adkins, L. C., & Hill, R. C. (2011). Using Stata for principles of econometrics. John Wiley & Sons.
5. Box, G., & Jenkins, G. M. (1976). Analysis: Forecasting and Control. San Francisco.
6. Chen, R. J. C., Bloomfield, P., & Cubbage, F. W. (2008). Comparing forecasting models in tourism. Journal of Hospitality & Tourism Research, 32(1), 3–21.
7. Cho, V. (2001). Tourism forecasting and its relationship with leading economic indicators. Journal of Hospitality & Tourism Research, 25 (4), 399–420.
8. Chu, F.-L. (2009). Forecasting tourism demand with ARMA-based methods. Tourism Management, 30(5), 740–751.
9. Goh, C., & Law, R. (2002). Modeling and forecasting tourism demand for arrivals with stochastic nonstationary seasonality and intervention. Tourism Management, 23(5), 499–510.
10. Gujarati, D. N., & Porter, D. C. (2004). Basic econometrics. mcgraw-hill companies. New York, NY, USA.
11. Karadzic, V., & Pejovic, B. (2020). Tourism demand forecasting using Arima model. Transformations in Business & Economics, 19.
12. Lim, C., & McAleer, M. (2002). Time series forecasts of international travel demand for Australia. Tourism Management, 23(4), 389–396.
13. Petrevska, B. (2017). Predicting tourism demand by ARIMA models. Economic Research-Ekonomska Istraživanja, 30(1), 939–950.
14. Song, H., & Li, G. (2008). Tourism demand modelling and forecasting A review of recent research. Tourism Management, 29(2), 203–220.
15. Song, H., Wen, L., & Liu, C. (2019). Density tourism demand forecasting revisited. Annals of Tourism Research, 75, 379–392.
16. Hai, T. T. M., & Vu, M. A. (2025). Forecasting Gold Price Trends in Vietnam in the Fourth Quarter of 2025 Using the Arima Model.